There’s power in knowing where potentially anything in the world is."

—Greg Milner, journalist and author

What is GPS?

GPS (Global Positioning System) is essentially a highly reliable signal sent from space that carries two critical pieces of information: location and time.

What is GPS used for?

The sky is really the limit on what you can do with GPS.

Some examples of GPS application include:

How does GPS work?

The basic methodology of GPS:

There are four key elements to making GPS work:

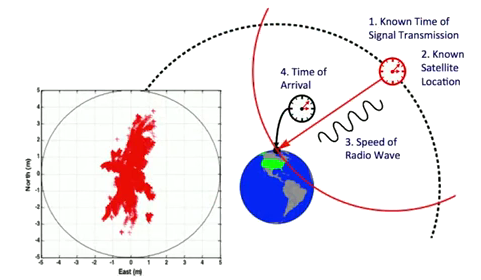
Elements of GPS. Image modified from “1.6 Satellites” in GPS: An Introduction to Satellite Navigation. Stanford University. 2016. https://youtu.be/2wbrN0pag7w

  1. Known transmission time
    • based on high-precision clocks and Einstein’s theory of general (time travels faster under lower gravity) and special relativity
  2. Known satellite location
    • based on globally distributed reference networks and Newtonian physics
  3. Speed of radio wave
    • very close to the speed of light (1 foot per nanosecond)
  4. Time of arrival
    • based on correlation of spread spectrum signals

With these four key elements we can begin to solve the “pseudo-range” equation. It is called pseudo-range because it is not the true range, but is equal to the true range plus some bias (due to the differences in time between the satellite and user).

This distance defines a sphere around a satellite. When combined with three more satellite distances, these distances can pin-point a location.

Because GPS measures distance, it uses the method of trilateration, rather than triangulation, which is used by surveyors for measuring angles.

Image from GIS Geography (2016). https://gisgeography.com/wp-content/uploads/2016/11/GPS-Trilateration-Feature-678x322.png

Note than the receiver clock is not synchronized to the GPS time. The result of these asynchronous clocks is a bias.

The fact that GPS uses a pseudo-range rather than the true range allows for the user’s GPS receiver to function with a low-cost, low-precision clock. If this were not the case, the proliferation of GPS as we know it today would have never happened due to the incredible expense of high-precision clocks.

Because GPS receivers must solve for their time bias (at the extra expense of needing a fourth satellite), there is the added bonus that every GPS receiver has a measure of its exact time.

True range equation

At the very basic level, we are trying to estimate the true range (or distance) between the satellite and the receiver. This distance can be calculated (assuming a perfect vacuum between the satellite and receiver) as the following:

\(c \times \left( t_\mathrm{arrival} - t_\mathrm{transmit} \right) = d\)

where

  • \(t_\mathrm{arrival}\) is the time of arrival (clock time on the receiver when the message was received)
  • \(t_\mathrm{transmit}\) is the time of transmission (clock time on the satellite when the message originated)
  • \(d\) is the distance between the receiver and the satellite
  • \(c\) is the speed of light

Due to asynchronous receiver/satellite time, the bias affects the arrival time; therefore, the range equation becomes more like the following:

\(c \times \left( t_\mathrm{arrival} + t_\mathrm{bias} - t_\mathrm{transmit} \right) = d\)

where

  • \(t_\mathrm{bias}\) is the clock bias due to asynchronous receiver/satellite time

Pseudo-range equation

Due to the clock bias, there are four unknown variables to be solved for in the pseudo-range equation. These include the clock offset of the user’s receiver (i.e., the bias) and the \(x\), \(y\) and \(z\) coordinates of the user’s location (i.e., the latitude, longitude and altitude). Because there are four unknowns, the user must have links with at least four different GPS satellites (known as a “lock” or “fix”).

\(\tau_{c}(t) = \left( \frac{d_{u}^{(k)}}{c} + b_u - \delta B^{(k)} \right) + \delta I_u^{(k)} + \delta T_u^{(k)} + \nu_u^{(k)}\)

\(d_u^{(k)} = \sqrt{\left( x_u - x^{(k)} \right)^2 + \left( y_u - y^{(k)} \right)^2 + \left( z_u - z^{(k)} \right)^2}\)

where:

  • \(b_u\) is the clock offset of the user clock relative to GPS system time (unknown)
  • \(\left(x_u, y_u, z_u \right)\) is the user’s location (unknown)

How do we find the satellites?

The known location of the GPS satellites is key for how GPS works.

The science behind satellite locations comes, in part, from our understanding of planetary orbits as described by Johannes Kepler (1571–1630) in his three laws. Kepler’s laws were further developed by Issac Newton (1642–1727), who drafted the governing equation in his law of gravity. Satellite operators across a global network of observation stations receive measurements from satellites to determine their locations. Using Newtonian physics, future satellite locations can be predicted based on their current position.

A brief history of GPS

The US Navy launched the first satellite-based geopositioning system (the predecessor of our modern-day GPS) in 1959, called the TRANSIT system.

Today’s modern GPS went from concept to realization in the 1970s under the direction of Brad Parkinson who was integral in the creation of the NAVSTAR program, which is now known as the Global Positioning System.

In 1978, the first “portable” GPS receiver was created; it was a backpack unit weighing in at around 25 pounds.

In 1989, the first commercial handheld GPS receiver was introduced (Magellan, copyright 2017 MiTAC International Corporation), which cost about $1000.

In 1999, the first commercially available GPS phone is released (Benefon Esc!).

In 2005, GPS becomes integrated into smartphones, which utilize a GPS-embedded chip that costs about $1.

The Global Positioning System

The Global Positioning System is comprised of three main segments:

Space
the satellites
Control
the worldwide monitoring and control stations
User
the signal receivers

Space Segment

In the United States, GPS satellites fly at an altitude of about 12,500 miles. The satellites make up a constellation, a series of satellites working together for a common purpose, that are arranged in six equally-spaced orbital planes surrounding Earth. Each plane consists of four “slots” that make up a 24-satellite arrangement that ensures that a GPS receiver on the ground can get a lock, or a fix on at least four satellites. As of October 17, 2017, there were a total of 31 operational satellites in the GPS constellation. (https://www.gps.gov/systems/gps/space/)

The GPS satellite constellation. Image from media.defense.gov (2018). https://media.defense.gov/2010/Feb/25/2000391199/-1/-1/0/100225-F-JZ027-160.JPG

A Message From Space

The satellite’s radio transmission is comprised of two parts (both are transmitted simultaneously):

  1. Navigation Message
  2. Navigation Signal

The navigation message is one of the two threads of data transmitted by the GPS satellites. The message consists of five subframes:

  1. Satellites health condition (clock status and correction)
  2. Satellite ephemeris (1/2)
  3. Satellite ephemeris (2/2)
  4. Satellite almanac (1/2)
  5. Satellite almanac (2/2)

The navigation signal includes the carrier and the code. The carrier is characterized by its frequency or wavelength. GPS signals are transmitted at certain frequencies. For example: GPS L1 has a frequency of 1.57542 GHz and GPS L2 has a frequency of 1.2276 GHz.

The code is used to identify which satellite is transmitting. This is accomplished by using pseudo-random numbers (PRN) to identify individual satellites. Each GPS receiver has a list of PRNs that align with the code sent from a given satellite.

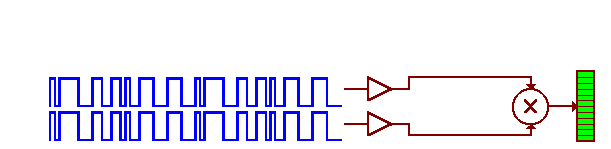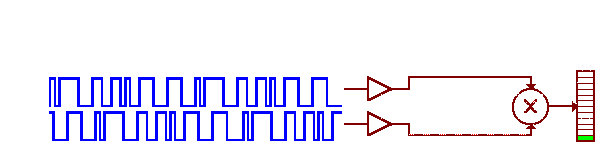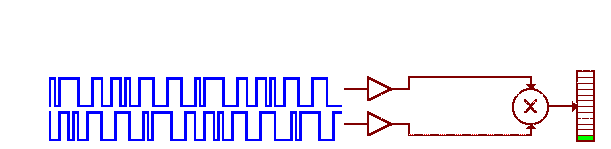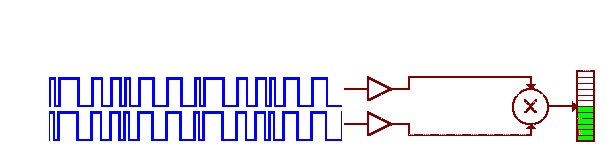
PRN correlation animation used to identify GPS satellites. Image by The Geographer’s Craft Project, Department of Geography, The University of Colorado at Boulder (2015). Online. https://www.colorado.edu/geography/gcraft/notes/gps/gif/bitsanim.gif

Control Segment

A reference network that continuously monitors the exact locations of the GPS satellite constellation. The locations of these ground stations are well known. To determine the locations of the satellites, it is the case of solving the GPS problem in reverse. These locations are then transmitted back to the satellites, such that this information can be re-transmitted back down to user GPS receivers.

The original GPS locations were in Hawaii (Eastern Pacific), Schriever U.S. Air Force Base in Colorado (North America), Ascension Island (South Atlantic), Diego Garcia (Indian Ocean), and Kwajalein (Western Pacific).

Over time, this original network has been augmented with additional stations.

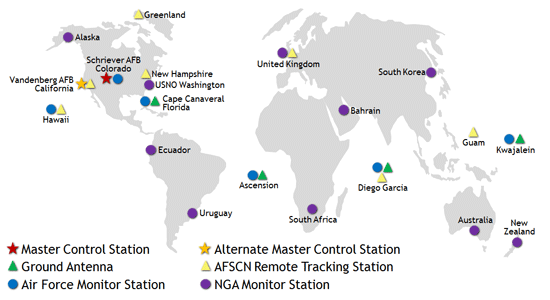
The GPS operation “ground” control segment. Image from www.gps.gov (2018). https://www.gps.gov/systems/gps/control/map.png

One of the most important aspects of the control segment is keeping GPS time. The GPS system time is the synchronized time that all satellites share. Small differences can occur between GPS time and the satellite clock. Corrections can be handled either digitally (accounted for through the GPS signal) or physically (an actual change to the satellite clock).

User Segment

Similar to the Internet, GPS has become an essential part of the global information infrastructure. The free, open, and dependable nature of GPS has led to the development of hundreds of applications affecting every aspect of modern life. GPS technology is now in everything from cell phones and wristwatches to construction equipment, shipping containers, and ATM’s. (https://www.gps.gov/applications/)

Glossary

A-GPS
  • Assisted Global Positioning System (GPS)
  • uses the range from GPS satellites, but receives the data (clock and satellite almanac) from a land-based cellular network to improve the time for GPS signal lock
Apogee
  • the proximal point in an object’s orbit; in the case of GPS, it is the point along the satellite’s orbit where it is closest to Earth
ARNS
  • Aeronautical Radio Navigation Signal
  • a band of the radio spectrum allocated for aviation
ASV
  • Autonomous Surface Craft
bands
  • radio bands (or frequency bands) are used to break up the RF spectrum into nominal frequencies for transmitting information; these bands are then allocated to certain services
C/A
  • Course Acquisition (or Clear Access)
  • a navigation signal code sent from GPS satellites
Clock Phase
  • the quantity that results when a flow or a rate is accumulated or summed
Clock Rate
  • the difference between two phase measurements divided by the duration of time that lapsed between taking the two measurements
Constellation
  • a system of satellites that work together to achieve a single purpose
  • also called a “satellite swarm”
DGPS
  • Differential Global Positioning Systems
EHF
  • Extremely High Frequency
  • RF band (30 GHz–300 GHz)
EGNOS
  • European Geostationary Navigation Overlay Service
  • European SBAS
Geodesy
  • a scientific discipline dealing with the measurement and representation of the Earth, primarily: Earth’s shape, gravity field, and orientation in space
  • it includes the quantification of properties of Earth’s surface and subsurface (e.g., crustal motion, ice sheets, glaciers, ocean tides and atmosphere)
  • it utilizes GPS to continuously monitor changes in these properties
GIS
  • Geographic Information System
  • visualization and analysis tool
GLONASS
  • transliteration: Globalnaya Navigazionnaya Sputnikovaya Sistema (Global Navigation Satellite System)
  • Russia’s version of GPS
GNSS
  • Global Navigation Satellite System
  • Special Topic: used in remote sensing (GNSS-R)
GPS
  • Global Positioning System
  • data collection tool
HF
  • High Frequency
  • RF band (3 MHz–30 MHz)
L1
  • Link 1
  • GPS navigation signal frequency (1.57542 GHz)
  • most commonly used GPS signal (supports 2–3 billion civilian receivers)
L2
  • Link 2
  • GPS navigation signal frequency (1.2276 GHz)
  • first used in 2005
  • used by both civilian and military receivers
  • provides a “backup” signal in the event L1 is unusable
  • combined with L1, it helps cancel out the largest error source from the GPS signal
LEO
  • Low Earth Orbit
  • this is where surveillance and spy satellites are located; it is closer to Earth than MEO, which allows for quality photographs of the surface to be taken
LF
  • Low Frequency
  • RF band (30–300 kHz)
Lock (or Fix)
  • when a GPS receiver has a lock or fix, there are at least four satellites in good view in order to provide an accurate account of location and time
MEO
  • Mean Earth Orbit
  • this is where the majority of GPS satellites are located; it is farther away than LEO, which provides about 1/3 of Earth’s surface in view of each satellite, reducing the total number of satellites required for global coverage
MF
  • Medium Frequency
  • RF band (300–3,000 kHz)
MSAS
  • Multi-functional Satellite Augmentation System
  • Japanese SBAS
Multipath Error
  • occurs when multiple instances of the same GPS signal are collected at a receiver due to the signal bouncing off obstructions (e.g., trees, buildings, other tall objects)
NMEA
  • National Marine Electronics Association
  • develop specifications (format) for communicating GPS data
NOAA
  • National Oceanic and Atmospheric Administration
Perigee
  • the extreme point in an object’s orbit; in the case of GPS, it is the point along the satellite’s orbit where it is farthest from Earth
Phase Cycle
  • the periodic reset of a Clock Phase
PRN
  • Pseudo Random Number
  • unique numeric look-up value assigned to satellites
Pseudo Range
  • distance calculated between a GPS receiver and a satellite with the presence of a phase error between the two clocks
QNSS
  • three frequencies patterned to complement GPS
Range
  • distance between GPS receiver and a satellite
Rate
  • the distance traveled over a given amount of time; a velocity
RF
  • Radio Frequency
RNSS
  • Radio Navigation Satellite System
  • a band of the radio spectrum allocated for navigation satellites
  • includes GPS L1 and L2 frequencies
ROV
  • Remotely Operated Vehicle
PNT
  • Position, Navigation and Timing
  • services provided by GPS
SBAS
  • Satellite-Based Augmentation Systems
  • complementary to GNSS; SBAS is a system of satellites and ground stations that provide GPS signal corrections to compensate GNSS accuracy, integrity, continuity and availability
  • provides location accuracy within 3 meters
  • see also EGNOS, MSAS and WAAS
SHF
  • Super High Frequency
  • RF band (3 GHz–30 GHz)
SV
  • Space Vehicle
  • another name for satellite
TTFF
  • Time To First Fix
  • the time it takes for a GPS receiver takes to accurately compute your position and time using at least four satellites after it is powered on
UHF
  • Ultra High Frequency
  • RF band (300 MHz–3,000 MHz)
UNAVCO
  • Originated as the University NAVSTAR Consortium in 1984; it is a non-profit university-governed consortium that facilitates geoscience research and education using geodesy
USV
  • Unmanned Surface Vehicle
VHF
  • Very High Frequency
  • RF band (30 MHz–300 MHz)
  • This band carried most early TV stations
WAAS
  • Wide Area Augmentation System
  • North American SBAS

Appendix

Einstein’s Theory of Relativity

Special Relativity
Time flows differently according to the state of motion (i.e., events that are simultaneous for one observer may not be for another). This is represented by the famous equation: \(E = m c^2\), which shows that mass increases with speed. A conclusion from this work is that time slows down for objects in motion.
General Relativity
The Principle of Equivalence that states that acceleration and gravity are indistinguishable. Massive objects cause a distortion in space-time, which is felt as gravity. As a result, time does not pass at the same rate for everyone. Under more gravitational force, time travels slower.

Kepler’s Three Laws

The Law of Ellipses
All planets orbit the sun in ellipses with the Sun located at one focus of the ellipse.

Figure. Kepler’s Law of Ellipses (Ventrudo 2013). Copyright 2008–2018 Mintaka Publishing Inc.

The Law of Equal Areas
A line joining a planet and the Sun sweeps out equal areas during equal intervals of time. This is because as a planet gets closer to the Sun, it has less potential energy and more kinetic energy (i.e., planets move faster when they are closer to the Sun).

Figure. Kepler’s Law of Equal Areas (Ventrudo 2013). Copyright 2008–2018 Mintaka Publishing Inc.

The Law of Harmonies
The square of the orbital period, \(P\), of a planet is directly proportional to the cube of the semi-major axis of its orbit, \(a\) (i.e., planets move slower when they are farther from the sun and whatever influence makes planets go around the sun weakens with distance).

\(P^2 \propto a^3\)

Keplerian Elements

The orbits of the satellites are described using six Keplerian elements.

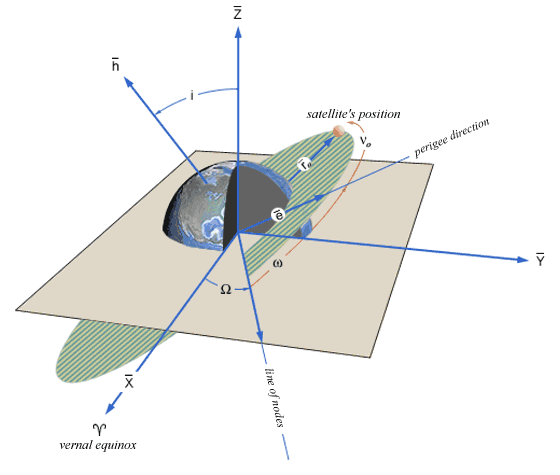
The Keplerian orbital parameters. Image modified from spaceflight.nasa.gov. Accessed 19 January 2018. https://spaceflight.nasa.gov/realdata/elements/graphs.html

where:

  • \(a\) is the semi-major axis of the orbit ellipse
  • \(e\) is the eccentricity of the ellipse
  • \(i\) is the inclination angle; describes the pitch between the satellite’s orbital plane (hashed) and Earth’s equatorial plane (gray)
  • \(\Omega\) is the angle of the right ascension of the ascending node; the angle between the vector connecting Earth’s center and the vernal equinox (along 0 degrees longitude at the Prime Meridian and 0 degrees latitude at the equator) and the vector connecting Earth’s center to the intersection of the equatorial and orbital planes
  • \(\omega\) is the angle of the perigee of the satellite orbit
  • \(\nu\) is the true anomaly; the angle describing the location of the satellite within its orbit with respect to the perigee

Newton’s Law of Gravity

Every point mass attracts every single other point mass by a force pointing along the line intersecting both points. The force is proportional to the product of the two masses and inversely proportional to the square of the distance between them (Newton 1687):

\(F = -\frac{G M m}{r^2}\)

where

  • \(F\) is the force of attraction between two bodies
  • \(M\) is the mass of one body
  • \(m\) is mass of the second body
  • \(r\) is the distance between two the bodies
  • \(G\) is the gravitational constant (6.674 N m2/kg2)

References

Newton, Isaac. 1687. Philosophiae Naturalis Principia Mathematica. London: Royal Society of London.

Ventrudo, Brian. 2013. “Kepler’s Laws.” https://oneminuteastronomer.com/8626/keplers-laws/.